In a type II superconductor, an external magnetic field applied to a sample penetrates in the form of quantized bundles of flux, known as flux or vortex lines[8]. These flux bundles are in fact topological defects very analogous to domain walls in Ising magnets. In the case of the superconductor, the order parameter is the complex ``pair wavefunction'' or gap
The macroscopic properties of most superconductors are well described
by a phenomenological expansion of the free energy in 
coupled
to the electro-magnetic field, known as Ginzburg-Landau theory
where 
, 
is the superconducting flux quantum. The factor of 2e in
reflects the charge of the singlet pair.
In the ordered phase at low temperatures, the coefficient 
is
large and negative, and develops an almost uniform amplitude. 
. The phase, however, can still vary in
space,
Up to a constant, the free energy becomes
A vortex is a configuration of 
which winds by 
around
some closed loop enclosing a singularity in the phase field (a
singularity is necessary since the phase must wind even as one shrinks
the path to a point). In three dimensions, these singularities take
the form of lines.
Let us now examine the magnetic flux passing through such a loop. At low temperatures, minimization of Eq. 115 requires
which, when integrated around the loop implies
Since the integral on the right hand side is just the flux through the loop, we have
Each vortex line therefore carries a quantum of magnetic flux (in fact, one may imagine vortex configurations with larger winding numbers, but these turn out to be energetically unfavorable, and split spontaneously into collections of fundamental vortices).
The density of vortices in the superconductor is determined by the magnitude of the applied field. Away from extremely low fields, where screening effects can be important, the vortex density adjusts so that there is one flux line per flux quantum, i.e.
where n is the areal density of vortex lines. If the magnetic field is fairly low, we may attempt to treat the vortices as independent. We'll return to the question of the behavior of the bulk system later.
If we assign an energy cost 
per unit length of the line,
a gradient expansion leads naturally to the random manifold elastic
energy (with d=1),
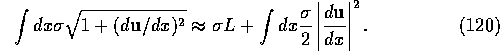
Disorder is always present in the form of atomic defects (probably dominant are oxygen vacancies in the doped cuprates) and larger defects such as grain boundaries, twin plans, screw dislocations... We will focus on the more microscopic point defects modeled phenomenologically by the random potential V.
So the vortex lines fit reasonably well into the framework of random manifolds. We therefore expect similar overall behavior, including the extremely slow response to an applied force. This is very important for the superconductors, because vortex motion is the main source of dissipation in these materials.
To understand this, suppose we run a (super) current through the
superconductor, perpendicular to the magnetic field axis. Because the
vortices carry a magnetic field, they exert a 
force
on the current. By Newton's third law, the vortices therefore
experience an equal and opposite force,
.
known as the Lorentz force. In the absence of disorder, this will
cause the vortex to move in the direction perpendicular to both 
and 
. Assuming a constant mobility 
(i.e. damping)
for the vortex, the asymptotic velocity
Since the vortex is magnetic, however this means that the system now has a time-varying magnetic field. By Faraday's law, this induces an electric field parallel to the current
The system therefore has a non-zero longitudinal dissipative resistivity.
When disorder is present, the vortices are pinned, and the effective
mobility is drastically reduced. In fact, since we expect v
to be exponentially small in f, the linear resistivity vanishes!
This slow ``creep'' motion discussed earlier was actually first
suggested in the context of flux motion in superconductors.
